Who would survive the Titanic?

There’s a practice exercise on Kaggle that gives Titanic passenger data and asks us to find the best predictor of survival. The exercise seems exciting, so, in this post, I will dive into Titanic data.

I will first present relationships between passengers’ attributes and their survival rate. Then, I’ll attempt to create a model for predicting survival. We’ll see what information matters and what doesn’t.

Data available

Kaggle gives data on a random sample of 2344 passengers: their class, age, family relationships, lodging, and general trip information.

Input data

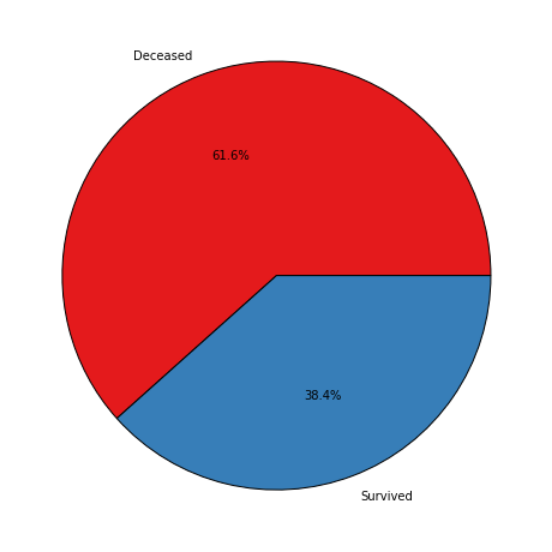
The general survival rate – the most important metric – rate was 38.4%.

Survival and death rates

Age, Gender, Wealth – basic correlations

Let’s see how important each attribute is on its own.

Age

Distribution of ages among survivors and victims

Note that around 20% of entries did not have the age attribute.

Gender

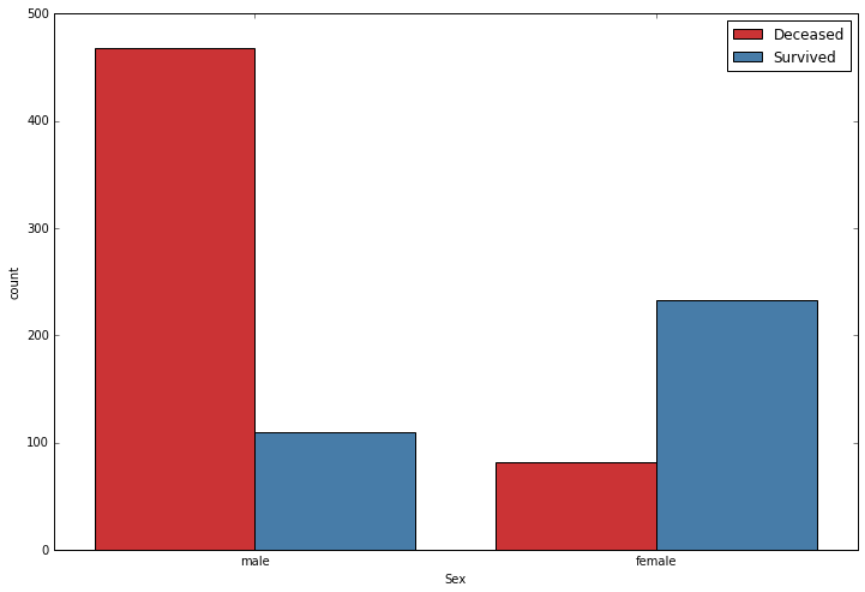Survival rate with respect to gender

Wealth

Survival rate with respect to class

Lodging

There were 8 main decks on Titanic: from A to G, and auxiliary decks like Tank deck.

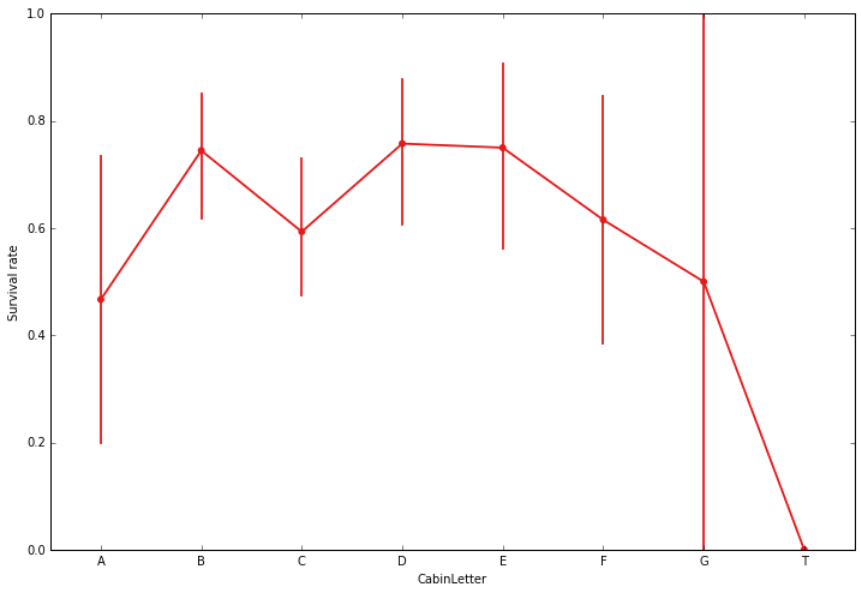Survival rate with respect to the cabin’s deck

Only 22.9% of passengers have cabin data in the sample, which explains why this attribute is highly biased.

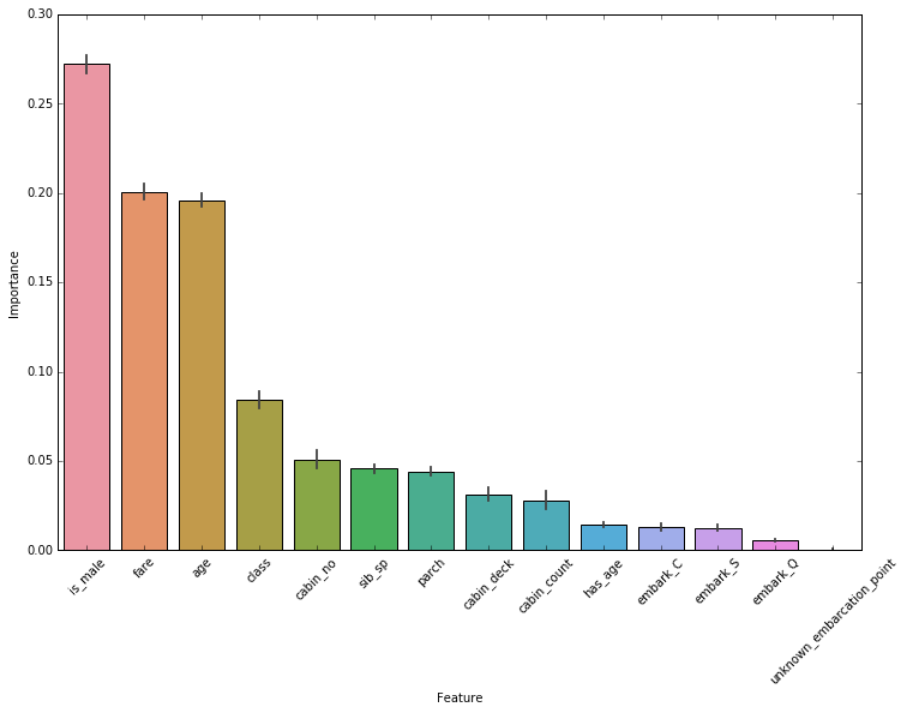
Feature importance

There are other meaningful features, but we covered the most interesting ones. Here’s a comparison of relative feature importances as measured using relative Gini importance.

Feature importance

Classification

I’ve tried using decision tree-based models as predictors. Note, that the base survival rate was 38%; even a classifier that always gives “Death” verdict would have 62% accuracy.

From the initial survey, it looks the gender is the best indicator of survival, and, indeed, a tree that just splits based on gender has 79% of estimated accuracy.

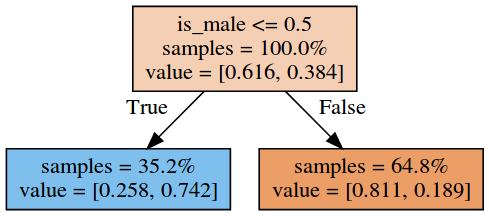A decision tree based on gender

Putting all data that is available in the input set doesn’t increase the estimate by much: only up to 82%. Here’s one of the best decision trees that I have trained:

One of the best decision trees.

The tree would predict that men with a cabin number and that are less than 36 years old would survive. According to the model, Women in the third class who embarked from Southampton would die.

I’ve also tried using more complicated models. A gradient boosted decision tree would get even 85% accuracy when measured using cross-validation.

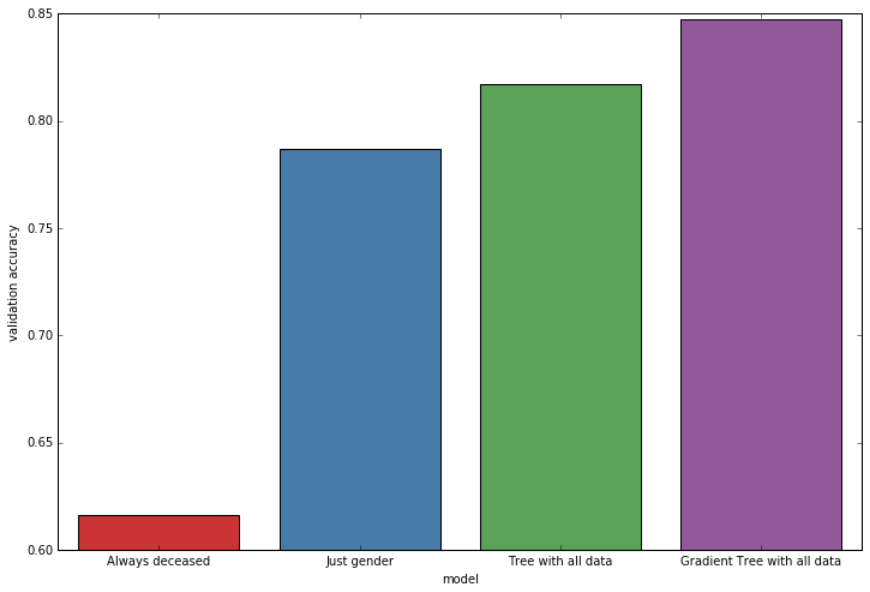Comparison of CV accuracy of all models

Verification with test data

I submitted results from all four models, and a surprising thing happened. The gradient boosted model performed worse than the gender-based tree. The likely explanation here is that I’ve been creating overfitted models.

Comparison of test accuracy of all models

Source

The Jupyter notebook I used for this analysis is available on Kaggle.