Profiling Haskell - fixing time and space leaks

In the previous post I have explained the rationale behind my Pentago game implementation. Here I will show how I have used Haskell’s profiling tools to uncover, understand, and fix serious time and space leaks inside that application.

Profiling mechanics

First off, let’s start with how basic profiling is done in haskell. The first step is to tell the compiler to add profiling functionality into the executable. If we were to compile directly via GHC we would add -prof -fprof-auto -rtsopts flags. With cabal the suggested method is to configure the entire build with

cabal configure --enable-executable-profiling

Or similarly with --enable-library-profiling flag if we are profiling a library. Be aware that profiling requires dependencies to be compiled with profiling support as well. Cabal installed libraries do not have that support on default therefore it is better to set such an option in ~/.cabal/config

library-profiling: True # uncomment

After we have built the library we can run it. To provide compiler options into an executable we have to wrap them into +RTS -RTS flags. So if we want our program to generate prog.prof file with profiling info we type:

./Pentago +RTS -p

Additionally we may want to collect extra information about memory usage. Some useful flags are:

-hc # add memory size produced by cost center
-hr # add retainer information (memory per function which holds it)
-hy # add type information of memory used at given time

That memory information is basically a function from time to space. For example -hy shows how much memory is taken by given type at given time. It is saved into a .hp file which can be used to generate an image using hp2ps. Later I prefer to use ghostscript to generate an jpeg image:

gs -r1190x1684 -sDEVICE=jpeg -sOutputFile=Pentago.jpg - < Pentago.ps

If you want to know more I recommend reading GHC’s docs.

Time leak

In the last post I have explained how an AI player chooses his move. First the program generates a pruned game tree such that each edge represents a move and game states are in leaves. Now the AI player lazily assigns a score to a game state in each leaf and min-max algorithm with alpha-beta pruning is performed. The speed of this solution relies on the alpha-beta pruning where branches which can not generate a better move are not traversed.

Originally the evaluation by each player was done in an Applicative to facilitate different computation strategies which may not be completely pure, in the sense that they may, for example, require random number generator. So the code looked as follows:

type GameStateEvaluation s g = (GameState s, Applicative f) => s -> f Score

-- |Just check whether state is final and assign appropriate score
trivialEvaluation :: (GameState s, Applicative f) => GameStateEvaluation s f
trivialEvaluation s = case getResult s of
 Nothing -> pure $ 0.0
 Just WhiteWin -> pure $ 1.0
 Just BlackWin -> pure $ (-1.0)

-- |In given state play gameCount random games. Use the number of wins to
-- calculate the score
randomPlayEvaluation :: (GameState s, RandomGen g)
  => GameStateEvaluation s (State g)
randomPlayEvaluation state = do
  let gameCount = 10
  -- Play gameCount random games and get (finalGameState, result) pairs from
  -- each game
  plays <- Control.Monad.State.forM [1..gameCount] (\_ -> randomPlay board)
  let (whiteWins, blackWins) = Data.List.foldl' -- sum up number of wins
       (\acc (_, result) -> case result of
         WhiteWin -> swap ((+ 1) <$>  swap acc)
         BlackWin -> (+ 1) <$>  acc
         Draw -> acc)
       (0,0)
       plays
  -- Calculate the score
  return . fromFloat $ (whiteWins - blackWins) / gameCount

In order to facilitate this construction we need to define the evaluation tree to be Traversable and add a general function to evaluate tree given evaluation function.

instance Traversable (LeafValueTree e) where
  sequenceA (Leaf fv) = Leaf <$> fv
  sequenceA (Node xs) = Node <$> sequenceA fList -- xs :: [(e, T e (f v))]
    where
      efTList = map (fmap sequenceA) xs -- [(e, f T e v)]
      fList = map (\(e, fT) -> (\t -> (e, t)) <$> fT) efTList -- [f (e, T e v)]

evaluateTree :: (GameState s, Applicative f) => (s -> f Score)
  -> PentagoGameTree s
  -> f PentagoEvaluationTree
evaluateTree evaluateF gameTree = traverse evaluateF leafTree
  where
    leafTree = toLeafValueTree gameTree

This shows the power of Haskell’s glue. In a few lines we have defined how given a general function which returns a computation we can sequence this computation in a tree. For example, in case of random evaluation, the state of random generator after the evaluation of the first node will be used in the evaluation of the next node.

Unfortunately, although theoretically smooth and elegant, this solution is wrong. It does not behave the way we want it to and it causes the program to crash when pruning is set to large depth. The reason for this crash was stack overflow.

I was surprised by this, the whole beauty of min-max was that after evaluating each branch it can and should be discarded, we only keep the alpha-beta parameter for each level and that’s it. There should be nothing more memory intensive inside the application. To help debug this I used all profiling tools at my disposal to check my assumptions.

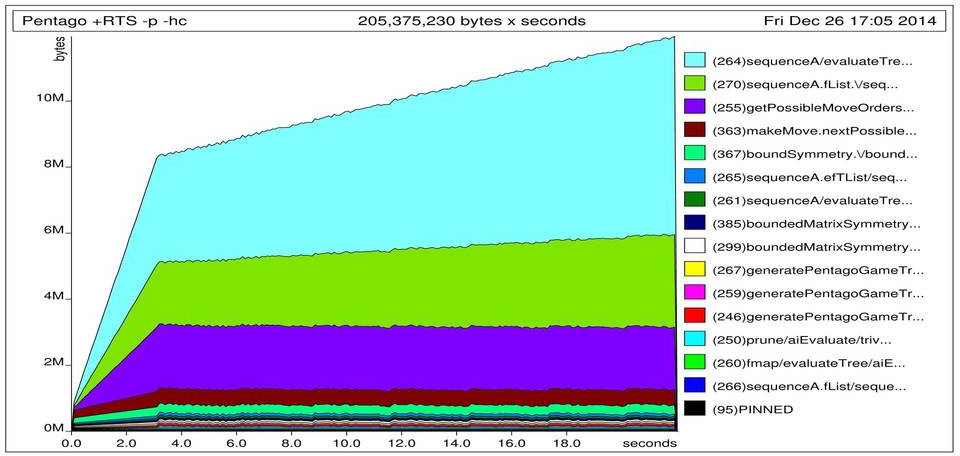
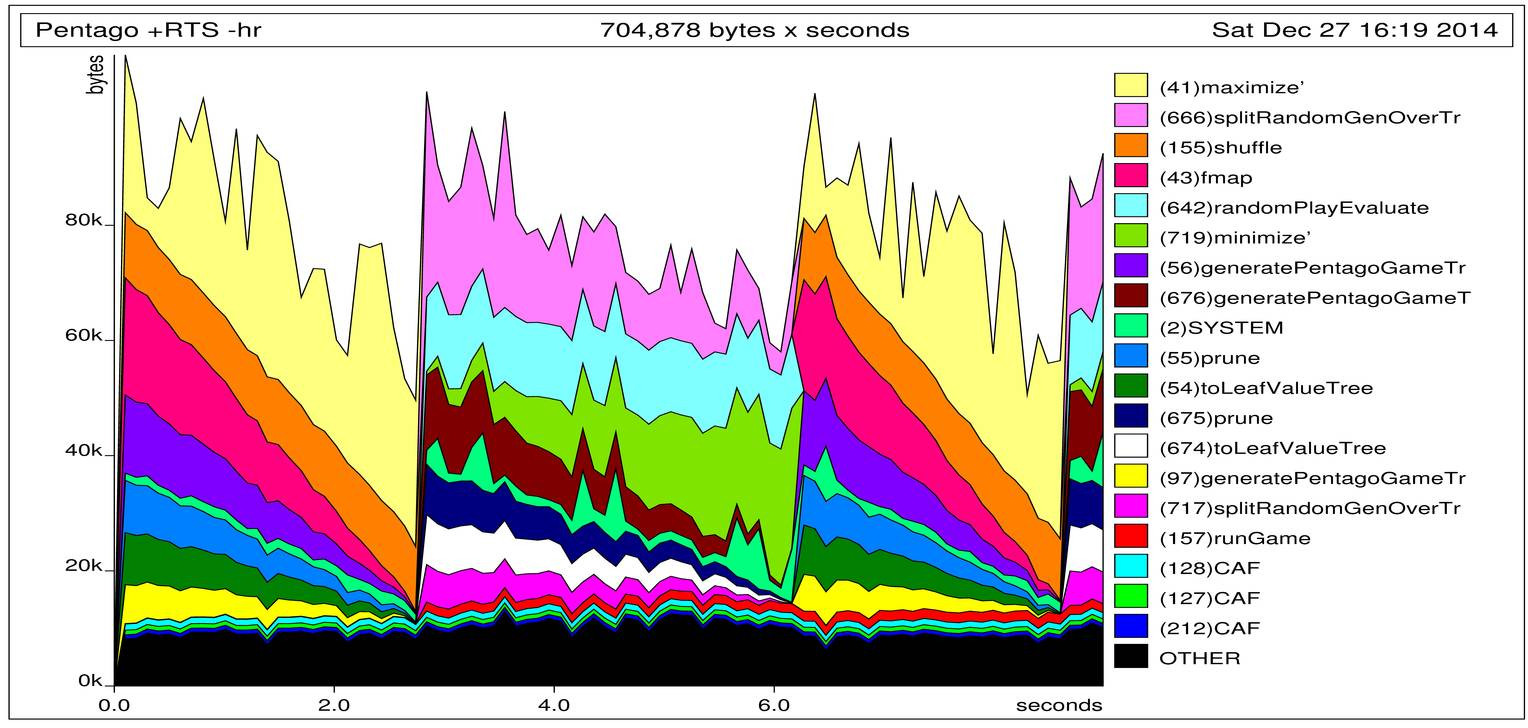
I checked how much memory I was using and which retainers kept it with +RTS -p -hr:

So after the first two seconds of computation there are 7MB of data kept by calls to sequenceA and later the SYSTEM data keeps growing until the stack overflows. I didn’t know at the time what SYSTEM data would consist of. Later we will find out that those are thunks.

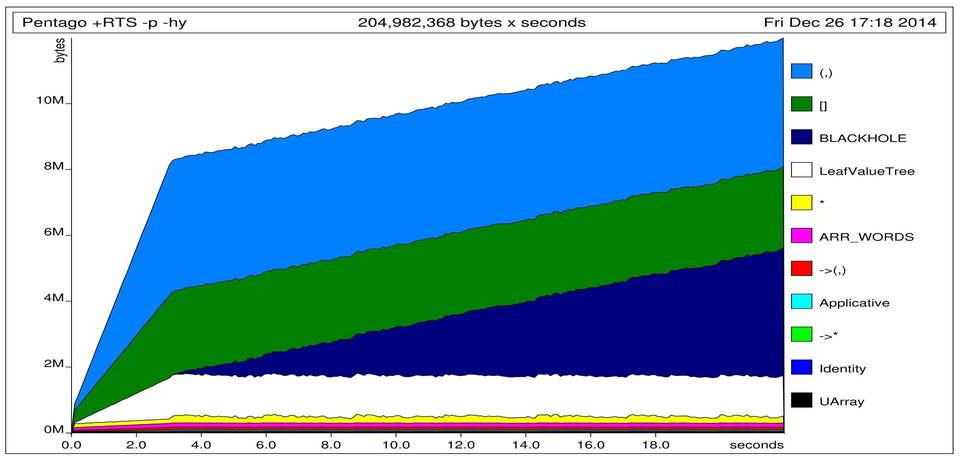
Ok, so we now know that SYSTEM keeps the memory that’s causing the stack to overflow. So which function generates this memory and of what type is it? Here options -hc and -hy will help us out.

So from the -hc graph we can conclude that the space leak is generated when evaluating the tree that is assigning scores to game states. The -hy graph shows that the offending memory is of type BLACKHOLE. After quick Google check I learned that this corresponds to thunks. That means that we generate a large thunk somewhere which we later try to normalize to weak head normal form. This is similar to a situation where we run a lazy fold like so:

foldl (+) 0 [1 .. 100000000]

This should cause out of memory exception and the reason can be found in this stackoverflow post.

One final clue I needed to locate this leak was the fact that when I have set up two ai players, one which used random evaluation with large depth and the other that used trivial evaluation with moderate depth then I occasionally I would see the random player move quickly while the trivial one would take a long time.

That might mean that the trivial player needs to evaluate something that is left by the random player. After some deliberation an idea struck me. Look carefully into what traverse does for random player. It composes execution of state monads inside leaves so that the state monad inside leaves is lifted to the level of a tree. Now, after performing min max on that tree what happens when we want to get the state after evaluation? Notice that the state after evaluation is defined as a state after evaluating each node in a tree. Therefore, even if min-max requires a score from only a subset of branches we, we still need to evaluate each leaf to get current state!

We need to refactor our program so that it works as we want it to. We do not really want to maintain proper state composition. In fact we do not care about the state at all. We use the State type as a convenience. What we really require is a random number generator when evaluating each node. My solution uses splits a random generator and attaches it to each node. Here’s the corrected code:

type GameStateEvaluation g = s -> Score

-- |Attach random generator to each leaf in a tree
splitRandomGenOverTree :: (RandomGen g)
  => g
  -> LeafValueTree e s
  -> LeafValueTree e (s, g)
splitRandomGenOverTree g (Leaf s) = Leaf (s, g)
splitRandomGenOverTree g (Node xs) = Node $
  fmap fst . tail $ scanl scanF (undefined, g) xs
  where
    scanF (_, g) (e, t) = ((e, splitRandomGenOverTree g0 t), g1)
      where (g0, g1) = split g

evaluateTree :: (s -> Score) -> LeafValueTree MoveOrder s -> PentagoEvaluationTree
evaluateTree evaluateF = fmap evaluateF

randomPlayEvaluate :: (GameState s, RandomGen g)
  => GameStateEvaluation (s, g)
randomPlayEvaluate (state, gen) = fst $ runState (do
  let gameCount = 2
   plays <- Control.Monad.State.forM [1..gameCount] (\_ -> randomPlay state)
  let (whiteWins, blackWins) = Data.List.foldl' -- sum up number of wins
       (\acc (_, result) -> case result of
         WhiteWin -> swap ((+ 1) <$>  swap acc)
         BlackWin -> (+ 1) <$>  acc
         Draw -> acc)
       (0,0)
       plays
  return . fromFloat $ (whiteWins - blackWins) / gameCount)
  gen

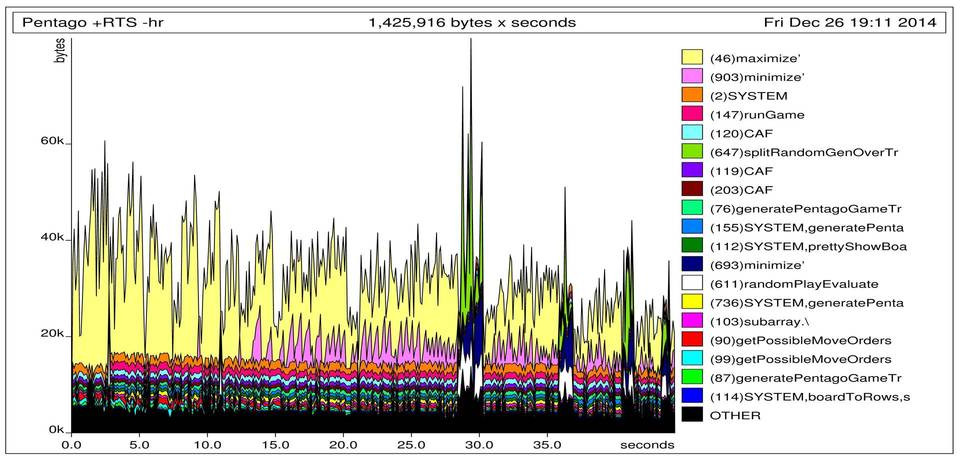
Now we do not compose monads. We only apply evaluate function from leaf node value to score. This allows us to use functor which does not compose and therefore facilitates pruning. The resulting memory footprint looks as follows:

60KB to evaluate around \(288^4\) nodes - so much better.

Space leak

The next day I decided to add move shuffling to tree evaluation. What that means is that in a tree I would shuffle the order of subtrees. This simple idea helps in with the alpha-beta pruning, because it allows completely different moves to be evaluated first. Using predetermined order meant that each move from left to right would be checked in order. If good moves were to lie only in the end of that order then alpha-beta pruning would be of little use in such a case.

Here’s the code that I have originally used:

shuffle' :: (RandomGen g) => [a] -> g -> ([a], g)

shuffle :: (RandomGen g) => [a] -> State g [a]
shuffle [] = return []
shuffle xs =
  let n = length xs
      indexes = [0..(n - 1)]
      xsArray = Data.Array.array (0, (n - 1)) (zip indexes xs)
  in do
    gen <- get
    let
      (orderList, newGen) = shuffle' indexes gen
      newXs = map (\i -> xsArray ! i) orderList
    put newGen
    return newXs

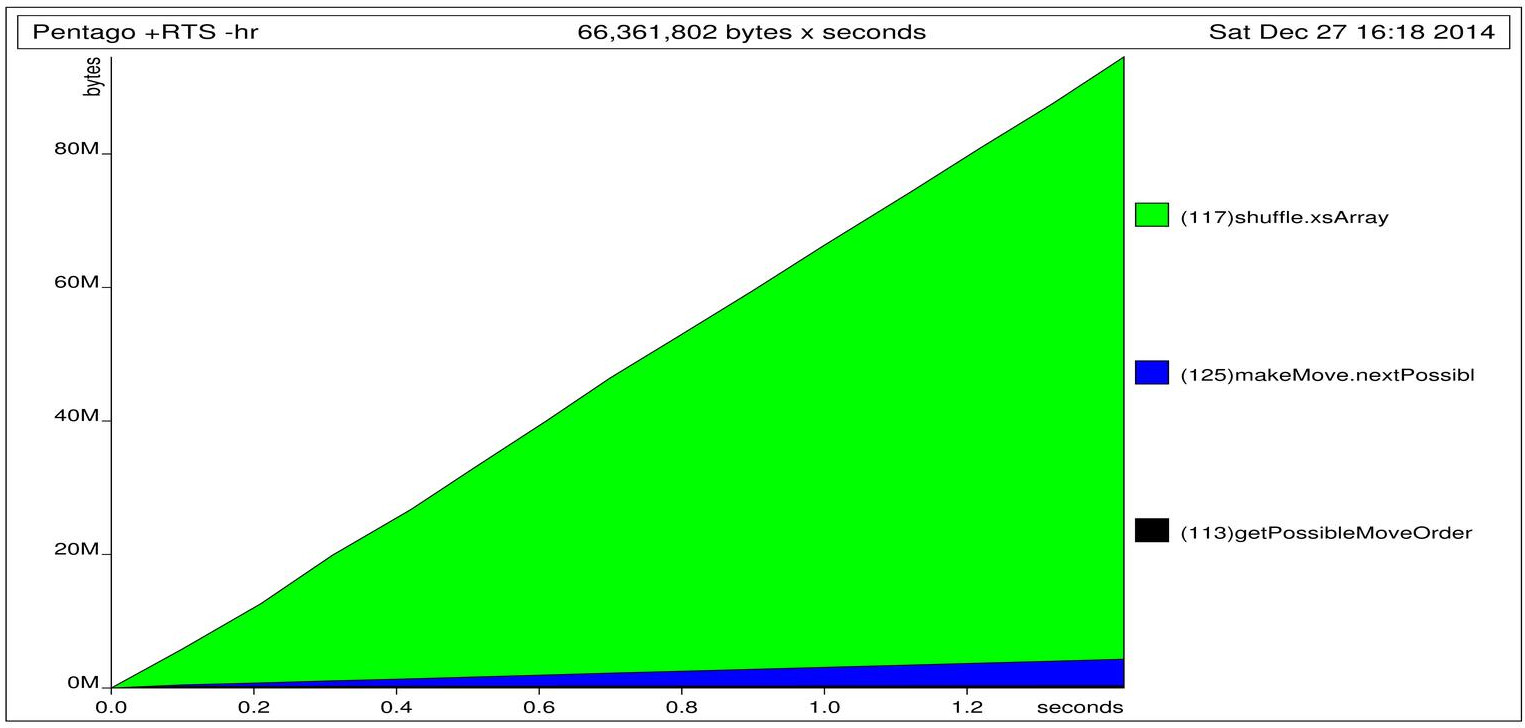
This would cause an out of memory crash:

I encourage you to find the reason in the above code before reading further.

The cause for this leak is in the definition of newXS. Again, the algorithm relies on garbage collection of evaluated subtrees, however in our shuffle the newXS in weak head normal form is a list of thunks: (\i -> xsArray ! i). So until after we evaluate every thunk those thunks will require the haskell runtime to keep original xsArray, that is all subtrees. This is not what we want, even though we shuffle the array, what we want is for the garbage collector to collect each element that has been traversed. Therefore once all those thunks come into existence, we need to shallowly evaluate them so that xsArray is not needed. Changing the return line achieves it.

return $ forceList newXs `seq` newXs

And all is fixed: